<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 3.2 Final//EN">
<!--Converted with LaTeX2HTML 2002-2-1 (1.71)
original version by: Nikos Drakos, CBLU, University of Leeds
* revised and updated by: Marcus Hennecke, Ross Moore, Herb Swan
* with significant contributions from:
Jens Lippmann, Marek Rouchal, Martin Wilck and others -->
<HTML>
<HEAD>
<TITLE>Power conservation and complex delay networks</TITLE>
<META NAME="description" CONTENT="Power conservation and complex delay networks">
<META NAME="keywords" CONTENT="book">
<META NAME="resource-type" CONTENT="document">
<META NAME="distribution" CONTENT="global">
<META NAME="Generator" CONTENT="LaTeX2HTML v2002-2-1">
<META HTTP-EQUIV="Content-Style-Type" CONTENT="text/css">
<LINK REL="STYLESHEET" HREF="book.css">
<LINK REL="next" HREF="node111.html">
<LINK REL="previous" HREF="node109.html">
<LINK REL="up" HREF="node104.html">
<LINK REL="next" HREF="node111.html">
</HEAD>
<BODY >
<!--Navigation Panel-->
<A NAME="tex2html2199"
HREF="node111.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="file:/usr/local/share/lib/latex2html/icons/next.png"></A>
<A NAME="tex2html2193"
HREF="node104.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="file:/usr/local/share/lib/latex2html/icons/up.png"></A>
<A NAME="tex2html2187"
HREF="node109.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="file:/usr/local/share/lib/latex2html/icons/prev.png"></A>
<A NAME="tex2html2195"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="file:/usr/local/share/lib/latex2html/icons/contents.png"></A>
<A NAME="tex2html2197"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="file:/usr/local/share/lib/latex2html/icons/index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html2200"
HREF="node111.html">Artificial reverberation</A>
<B> Up:</B> <A NAME="tex2html2194"
HREF="node104.html">Time shifts and delays</A>
<B> Previous:</B> <A NAME="tex2html2188"
HREF="node109.html">Recirculating delay networks</A>
<B> <A NAME="tex2html2196"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html2198"
HREF="node201.html">Index</A></B>
<BR>
<BR>
<!--End of Navigation Panel-->
<H1><A NAME="SECTION001150000000000000000">
Power conservation and complex delay networks</A>
</H1>
<P>
The same techniques will work to analyze any delay network, although for
more complicated networks it becomes harder to characterize the results, or
to design the network to have specific, desired properties. Another point
of view can sometimes be usefully brought to the situation, particularly
when flat frequency responses are needed, either in their own right or else
to ensure that a complex, recirculating network remains stable at feedback
gains close to one.
<P>
The central fact we will use is that if any delay network, with either one or
many inputs and outputs, is constructed so that its output power
(averaged over time) always
equals its input power, that network has to have a flat frequency response.
This is almost a tautology; if you put in a sinusoid at any frequency on one of
the inputs, you will get sinusoids of the same frequency at the outputs, and
the sum of the power on all the outputs will equal the power of the input, so
the gain, suitably defined, is exactly one.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.11"></A><A NAME="8003"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.11:</STRONG>
First fundamental building block for unitary delay networks:
delay lines in parallel.</CAPTION>
<TR><TD><IMG
WIDTH="126" HEIGHT="170" BORDER="0"
SRC="img737.png"
ALT="\begin{figure}\psfig{file=figs/fig07.11.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
In order to work with power-conserving delay networks we will need an
explicit definition of ``total average power".
If there is only one signal (call it <IMG
WIDTH="31" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img80.png"
ALT="$x[n]$">), the average power is
given by:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
P(x[n]) = \left [{{|x[0]|}^2} + {{|x[1]|}^2} + \cdots
+ {{|x[N-1]|}^2} \right ] / N
\end{displaymath}
-->
<IMG
WIDTH="349" HEIGHT="34" BORDER="0"
SRC="img738.png"
ALT="\begin{displaymath}
P(x[n]) = \left [{{\vert x[0]\vert}^2} + {{\vert x[1]\vert}^2} + \cdots
+ {{\vert x[N-1]\vert}^2} \right ] / N
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
where <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img3.png"
ALT="$N$"> is a large enough number so that any fluctuations in amplitude get
averaged out. This definition works as well for complex-valued signals
as for real-valued ones. The average total power for several digital
audio signals is
just the sum of the individual signal's powers:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
P({x_1}[n] , \ldots , {x_r}[n]) = P({x_1}[n]) + \cdots + P({x_r}[n])
\end{displaymath}
-->
<IMG
WIDTH="326" HEIGHT="28" BORDER="0"
SRC="img739.png"
ALT="\begin{displaymath}
P({x_1}[n] , \ldots , {x_r}[n]) = P({x_1}[n]) + \cdots + P({x_r}[n])
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
where <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img467.png"
ALT="$r$"> is the number of signals to be combined.
<P>
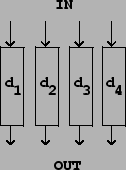
It turns out that a wide range of interesting delay networks has the property
that the total power output equals the total power input;
they are called
<A NAME="8013"></A><I>unitary</I>. To start with, we can put any number of delays in parallel, as
shown in Figure <A HREF="#fig07.11">7.11</A>. Whatever the total power of the inputs,
the total power of the outputs has to equal it.
<P>
A second family of power-preserving transformations is composed of rotations
and reflections of the signals <IMG
WIDTH="38" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img740.png"
ALT="${x_1}[n]$">, ... , <IMG
WIDTH="38" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img741.png"
ALT="${x_r}[n]$">, considering them,
at each fixed time point <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img75.png"
ALT="$n$">, as the <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img467.png"
ALT="$r$"> coordinates of a point in
<IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img467.png"
ALT="$r$">-dimensional space. The rotation or reflection must be one that leaves the
origin <!-- MATH
$(0, \ldots, 0)$
-->
<IMG
WIDTH="67" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img742.png"
ALT="$(0, \ldots, 0)$"> fixed.
<P>
For each sample number <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img75.png"
ALT="$n$">, the total
contribution to the average signal power is proportional to
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{|{x_1}|}^2 + \cdots + {|{x_r}|}^2
\end{displaymath}
-->
<IMG
WIDTH="119" HEIGHT="28" BORDER="0"
SRC="img743.png"
ALT="\begin{displaymath}
{\vert{x_1}\vert}^2 + \cdots + {\vert{x_r}\vert}^2
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
This is just the Pythagorean distance from the origin to
the point <!-- MATH
$({x_1}, \ldots, {x_r})$
-->
<IMG
WIDTH="83" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img744.png"
ALT="$({x_1}, \ldots, {x_r})$">. Since rotations and reflections are
distance-preserving transformations, the distance from the origin before
transforming must
equal the distance from the origin afterward. So the total power
of a collection of signals must must be preserved by rotation.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.12"></A><A NAME="8024"></A>
<TABLE>
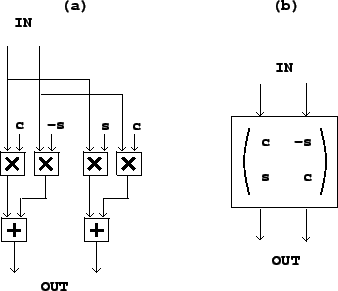<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.12:</STRONG>
Second fundamental building block for unitary delay networks:
rotating two digital audio signals. Part (a) shows the transformation explicitly;
(b) shows it as a matrix operation.</CAPTION>
<TR><TD><IMG
WIDTH="338" HEIGHT="291" BORDER="0"
SRC="img745.png"
ALT="\begin{figure}\psfig{file=figs/fig07.12.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
Figure <A HREF="#fig07.12">7.12</A> shows a rotation matrix operating on two signals. In
part (a) the transformation is shown explicitly. If the input signals are
<IMG
WIDTH="38" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img740.png"
ALT="${x_1}[n]$"> and <IMG
WIDTH="38" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img746.png"
ALT="${x_2}[n]$">, the outputs are:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{y_1}[n] = c {x_1}[n] - s {x_2}[n]
\end{displaymath}
-->
<IMG
WIDTH="156" HEIGHT="28" BORDER="0"
SRC="img747.png"
ALT="\begin{displaymath}
{y_1}[n] = c {x_1}[n] - s {x_2}[n]
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{y_2}[n] = s {x_1}[n] + c {x_2}[n]
\end{displaymath}
-->
<IMG
WIDTH="156" HEIGHT="28" BORDER="0"
SRC="img748.png"
ALT="\begin{displaymath}
{y_2}[n] = s {x_1}[n] + c {x_2}[n]
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
where <IMG
WIDTH="24" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img749.png"
ALT="$c, s$"> are given by
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
c = \cos(\theta)
\end{displaymath}
-->
<IMG
WIDTH="67" HEIGHT="28" BORDER="0"
SRC="img750.png"
ALT="\begin{displaymath}
c = \cos(\theta)
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
s = \sin(\theta)
\end{displaymath}
-->
<IMG
WIDTH="67" HEIGHT="28" BORDER="0"
SRC="img751.png"
ALT="\begin{displaymath}
s = \sin(\theta)
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
for an
<A NAME="8036"></A><I>angle of rotation</I> <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img634.png"
ALT="$\theta$">.
Considered as points on the Cartesian plane, the point <!-- MATH
$({y_1}, {y_2})$
-->
<IMG
WIDTH="52" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img752.png"
ALT="$({y_1}, {y_2})$"> is
just the point <!-- MATH
$({x_1}, {x_2})$
-->
<IMG
WIDTH="55" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img753.png"
ALT="$({x_1}, {x_2})$"> rotated counter-clockwise by the angle
<IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img634.png"
ALT="$\theta$">. The two points are thus at the same distance from the origin:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{|{y_1}|}^2 + {|{y_2}|}^2 = {|{x_1}|}^2 + {|{x_2}|}^2
\end{displaymath}
-->
<IMG
WIDTH="183" HEIGHT="28" BORDER="0"
SRC="img754.png"
ALT="\begin{displaymath}
{\vert{y_1}\vert}^2 + {\vert{y_2}\vert}^2 = {\vert{x_1}\vert}^2 + {\vert{x_2}\vert}^2
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
and so the two output signals have the same total power as the two input
signals.
<P>
For an alternative description of rotation in two dimensions,
consider complex numbers <!-- MATH
$X={x_1} + {x_2}i$
-->
<IMG
WIDTH="96" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img755.png"
ALT="$X={x_1} + {x_2}i$"> and
<!-- MATH
$Y={y_1} + {y_2}i$
-->
<IMG
WIDTH="92" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img756.png"
ALT="$Y={y_1} + {y_2}i$">. The above transformation amounts to setting
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
Y = XZ
\end{displaymath}
-->
<IMG
WIDTH="60" HEIGHT="24" BORDER="0"
SRC="img757.png"
ALT="\begin{displaymath}
Y = XZ
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
where <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img20.png"
ALT="$Z$"> is a complex number with
unit magnitude and argument <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img634.png"
ALT="$\theta$">. Since <IMG
WIDTH="53" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img22.png"
ALT="$\vert Z\vert=1$">, it follows that
<IMG
WIDTH="69" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img758.png"
ALT="$\vert X\vert = \vert Y\vert$">.
<P>
If we perform a rotation on a pair of signals and then invert one (but not the
other) of them, the result is a
<A NAME="8050"></A>
<I>reflection</I>.
This also preserves total signal power, since we can invert any or all of a
collection of signals without changing the total power. In two dimensions, a
reflection appears as a transformation of the form
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{y_1}[n] = c {x_1}[n] + s {x_2}[n]
\end{displaymath}
-->
<IMG
WIDTH="156" HEIGHT="28" BORDER="0"
SRC="img759.png"
ALT="\begin{displaymath}
{y_1}[n] = c {x_1}[n] + s {x_2}[n]
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{y_2}[n] = s {x_1}[n] - c {x_2}[n]
\end{displaymath}
-->
<IMG
WIDTH="156" HEIGHT="28" BORDER="0"
SRC="img760.png"
ALT="\begin{displaymath}
{y_2}[n] = s {x_1}[n] - c {x_2}[n]
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<P>
A special and useful rotation matrix is obtained by setting
<!-- MATH
$\theta = \pi/4$
-->
<IMG
WIDTH="58" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img34.png"
ALT="$\theta = \pi /4$">, so that <!-- MATH
$s = c = \sqrt{1/2}$
-->
<IMG
WIDTH="100" HEIGHT="38" ALIGN="MIDDLE" BORDER="0"
SRC="img761.png"
ALT="$s = c = \sqrt{1/2}$">. This
allows us to simplify the computation as shown in Figure <A HREF="#fig07.13">7.13</A> (part
a) because each signal need only be multiplied by the one quantity <IMG
WIDTH="39" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img762.png"
ALT="$c=s$">.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.13"></A><A NAME="8389"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.13:</STRONG>
Details about rotation (and reflection) matrix operations: (a)
rotation by the angle <!-- MATH
$\theta = \pi/4$
-->
<IMG
WIDTH="58" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img34.png"
ALT="$\theta = \pi /4$">, so that
<!-- MATH
$a = \cos(\theta) = \sin(\theta) = \sqrt{1/2} \approx 0.7071$
-->
<IMG
WIDTH="262" HEIGHT="38" ALIGN="MIDDLE" BORDER="0"
SRC="img763.png"
ALT="$a = \cos(\theta) = \sin(\theta) = \sqrt{1/2} \approx 0.7071$">; (b) combining
two-dimensional rotations to make higher-dimensional ones.</CAPTION>
<TR><TD><IMG
WIDTH="298" HEIGHT="296" BORDER="0"
SRC="img764.png"
ALT="\begin{figure}\psfig{file=figs/fig07.13.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
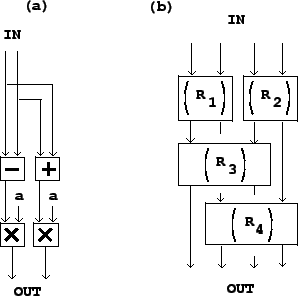More complicated rotations or reflections of more than two input signals may be
made by repeatedly rotating and/or reflecting them in pairs. For
example, in Figure <A HREF="#fig07.13">7.13</A> (part b), four signals are combined in
pairs, in two successive stages, so that in the end every signal input feeds
into all the outputs. We could do the same with eight signals (using three
stages) and so on. Furthermore, if we use the special angle <IMG
WIDTH="29" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img52.png"
ALT="$\pi /4$">, all the
input signals will contribute equally to each of the outputs.
<P>
Any combination of delays and rotation matrices, applied in succession to a
collection of audio signals, will result in a flat frequency response, since
each individual operation does.
This already allows us to generate an infinitude of
flat-response delay networks, but so far, none of them are recirculating. A
third operation, shown in Figure <A HREF="#fig07.14">7.14</A>, allows us to make
recirculating networks that still enjoy flat frequency responses.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.14"></A><A NAME="8069"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.14:</STRONG>
Flat frequency response in recirculating networks: (a) in general,
using a rotation matrix <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$">; (b) the ``all-pass" configuration.</CAPTION>
<TR><TD><IMG
WIDTH="381" HEIGHT="287" BORDER="0"
SRC="img765.png"
ALT="\begin{figure}\psfig{file=figs/fig07.14.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
Part (a) of the figure shows the general layout. The transformation <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> is
assumed to be any combination of delays and mixing matrices that preserves
total power. The signals <!-- MATH
${x_1}, \ldots {x_k}$
-->
<IMG
WIDTH="64" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img766.png"
ALT="${x_1}, \ldots {x_k}$"> go into a
unitary delay network, and the output signals <!-- MATH
${y_1}, \ldots {y_k}$
-->
<IMG
WIDTH="62" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img767.png"
ALT="${y_1}, \ldots {y_k}$"> emerge.
Some other signals <!-- MATH
${w_1}, \ldots {w_j}$
-->
<IMG
WIDTH="68" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img768.png"
ALT="${w_1}, \ldots {w_j}$"> (where <IMG
WIDTH="10" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img769.png"
ALT="$j$"> is not necessarily equal to
<IMG
WIDTH="12" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img58.png"
ALT="$k$">) appear at the output of the transformation <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> and are fed back to its
input.
<P>
If <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> is indeed power preserving, the total input power (the power of the
signals <!-- MATH
${x_1}, \ldots {x_k}$
-->
<IMG
WIDTH="64" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img766.png"
ALT="${x_1}, \ldots {x_k}$"> plus that of the signals <!-- MATH
${w_1}, \ldots {w_j}$
-->
<IMG
WIDTH="68" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img768.png"
ALT="${w_1}, \ldots {w_j}$">)
must equal the output power (the power of the signals <!-- MATH
${y_1}, \ldots {y_k}$
-->
<IMG
WIDTH="62" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img767.png"
ALT="${y_1}, \ldots {y_k}$">
plus <!-- MATH
${w_1}, \ldots {w_j}$
-->
<IMG
WIDTH="68" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img768.png"
ALT="${w_1}, \ldots {w_j}$">), and subtracting all the <IMG
WIDTH="15" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img770.png"
ALT="$w$"> from the
equality, we find that the total input and output power are equal.
<P>
If we let <IMG
WIDTH="70" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img771.png"
ALT="$j=k=1$"> so that there is one <IMG
WIDTH="12" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img243.png"
ALT="$x$">, <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img106.png"
ALT="$y$">, and <IMG
WIDTH="15" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img770.png"
ALT="$w$">,
and
let the transformation <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> be a rotation by <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img634.png"
ALT="$\theta$"> followed by a delay of
<IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img28.png"
ALT="$d$"> samples on the <IMG
WIDTH="20" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img31.png"
ALT="$W$"> output, the result is the well-known
<A NAME="8086"></A><A NAME="8087"></A><I>all-pass filter</I>.
With some juggling, and letting <!-- MATH
$c = \cos(\theta)$
-->
<IMG
WIDTH="73" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img772.png"
ALT="$c = \cos(\theta)$">, we can show it is
equivalent to the network
shown in part (b) of the figure. All-pass filters have many applications, some
of which we will visit later in this book.
<P>
<HR>
<!--Navigation Panel-->
<A NAME="tex2html2199"
HREF="node111.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="file:/usr/local/share/lib/latex2html/icons/next.png"></A>
<A NAME="tex2html2193"
HREF="node104.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="file:/usr/local/share/lib/latex2html/icons/up.png"></A>
<A NAME="tex2html2187"
HREF="node109.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="file:/usr/local/share/lib/latex2html/icons/prev.png"></A>
<A NAME="tex2html2195"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="file:/usr/local/share/lib/latex2html/icons/contents.png"></A>
<A NAME="tex2html2197"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="file:/usr/local/share/lib/latex2html/icons/index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html2200"
HREF="node111.html">Artificial reverberation</A>
<B> Up:</B> <A NAME="tex2html2194"
HREF="node104.html">Time shifts and delays</A>
<B> Previous:</B> <A NAME="tex2html2188"
HREF="node109.html">Recirculating delay networks</A>
<B> <A NAME="tex2html2196"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html2198"
HREF="node201.html">Index</A></B>
<!--End of Navigation Panel-->
<ADDRESS>
Miller Puckette
2006-12-30
</ADDRESS>
</BODY>
</HTML>