<!DOCTYPE html>
<!--Converted with LaTeX2HTML 2002-2-1 (1.71)
original version by: Nikos Drakos, CBLU, University of Leeds
* revised and updated by: Marcus Hennecke, Ross Moore, Herb Swan
* with significant contributions from:
Jens Lippmann, Marek Rouchal, Martin Wilck and others -->
<HTML>
<HEAD>
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<TITLE>Classical waveforms</TITLE>
<META NAME="description" CONTENT="Classical waveforms">
<META NAME="keywords" CONTENT="book">
<META NAME="resource-type" CONTENT="document">
<META NAME="distribution" CONTENT="global">
<META NAME="Generator" CONTENT="LaTeX2HTML v2002-2-1">
<META HTTP-EQUIV="Content-Style-Type" CONTENT="text/css">
<LINK REL="STYLESHEET" HREF="book.css">
<LINK REL="next" HREF="node201.html">
<LINK REL="previous" HREF="node163.html">
<LINK REL="up" HREF="book.html">
<LINK REL="next" HREF="node185.html">
</HEAD>
<BODY >
<!--Navigation Panel-->
<A ID="tex2html3311"
HREF="node185.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A ID="tex2html3305"
HREF="book.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A ID="tex2html3299"
HREF="node183.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A ID="tex2html3307"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A ID="tex2html3309"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A ID="tex2html3312"
HREF="node185.html">Symmetries and Fourier series</A>
<B> Up:</B> <A ID="tex2html3306"
HREF="book.html">book</A>
<B> Previous:</B> <A ID="tex2html3300"
HREF="node183.html">Exercises</A>
<B> <A ID="tex2html3308"
HREF="node4.html">Contents</A></B>
<B> <A ID="tex2html3310"
HREF="node201.html">Index</A></B>
<BR>
<BR>
<!--End of Navigation Panel-->
<H1><A ID="SECTION001400000000000000000"></A>
<A ID="chapter-waveforms"></A>
<BR>
Classical waveforms
</H1>
<P>
Up until now we have primarily taken three approaches to synthesizing
repetitive waveforms: additive synthesis (Chapter 1),
wavetable synthesis (Chapter <A HREF="node26.html#chapter-wavetable">2</A>), and waveshaping
(Chapters <A HREF="node75.html#chapter-modulation">5</A> and <A HREF="node89.html#chapter-paf">6</A>). This chapter
introduces a fourth
approach, in which waveforms are built up explicitly from line segments with
controllable endpoints. This approach is historically at least as important
as the others, and was dominant during the
analog synthesizer period, approximately 1965-1985.
For lack of a better name, we'll use the term
<A ID="14228"></A><I>classical waveforms</I>
to denote waveforms composed of line segments.
<P>
<DIV ALIGN="CENTER"><A ID="fig10.01"></A><A ID="14232"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 10.1:</STRONG>
Classical waveforms: (a) the sawtooth, (b) the triangle, and (c)
the rectangle wave,
shown as functions of a continuous variable (not sampled).</CAPTION>
<TR><TD><IMG
WIDTH="475" HEIGHT="351" BORDER="0"
SRC="img1249.png"
ALT="\begin{figure}\psfig{file=figs/fig10.01.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
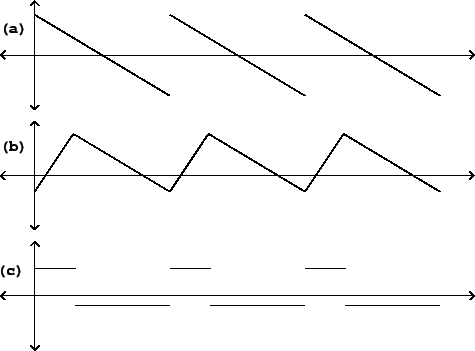
They include the
<A ID="14235"></A><A ID="14236"></A><A ID="14237"></A><I>sawtooth</I>, <I>triangle</I>, and <I>rectangle</I> waves pictured in Figure
<A HREF="#fig10.01">10.1</A>, among many other possibilities. The salient features of
classical waveforms are either discontinuous jumps (changes in value) or
corners (changes in slope). In the figure, the sawtooth and rectangle waves
have jumps (once per cycle for the sawtooth, and twice for the rectangle), and
constant slope elsewhere (negative for the sawtooth wave, zero for the
rectangle wave). The triangle wave has no discontinuous jumps, but the slope
changes discontinuously twice per cycle.
<P>
To use classical waveforms effectively, it is useful to understand how the
shape of the waveform is reflected in its Fourier series. (To compute these we
need background from Chapter <A HREF="node163.html#chapter-fft">9</A>, which is why this chapter
appears here and not earlier.) We will also need strategies for digitally
synthesizing classical waveforms. These waveforms prove to be much
more susceptible to foldover problems than any we have treated before, so we
will have to pay especially close attention to its control.
<P>
In general, our strategy for predicting and controlling foldover will be to
consider first those sampled waveforms whose period is an integer <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img3.png"
ALT="$N$">. Then if
we want to obtain a waveform of a non-integral period (call it <IMG
WIDTH="12" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img135.png"
ALT="$\tau$">, say) we
approximate <IMG
WIDTH="12" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img135.png"
ALT="$\tau$"> as a quotient <IMG
WIDTH="36" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img1250.png"
ALT="$N/R$"> of two integers. Conceptually at least,
we can then synthesize the desired waveform with period <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img3.png"
ALT="$N$">, and then take only
one of each <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> samples of output. This last, down-sampling step is where the
foldover is produced, and careful handling will help us control it.
<P>
<BR><HR>
<!--Table of Child-Links-->
<A ID="CHILD_LINKS"><STRONG>Subsections</STRONG></A>
<UL>
<LI><A ID="tex2html3313"
HREF="node185.html">Symmetries and Fourier series</A>
<UL>
<LI><A ID="tex2html3314"
HREF="node186.html">Sawtooth waves and symmetry</A>
</UL>
<BR>
<LI><A ID="tex2html3315"
HREF="node187.html">Dissecting classical waveforms</A>
<LI><A ID="tex2html3316"
HREF="node188.html">Fourier series of the elementary waveforms</A>
<UL>
<LI><A ID="tex2html3317"
HREF="node189.html">Sawtooth wave</A>
<LI><A ID="tex2html3318"
HREF="node190.html">Parabolic wave</A>
<LI><A ID="tex2html3319"
HREF="node191.html">Square and symmetric triangle waves</A>
<LI><A ID="tex2html3320"
HREF="node192.html">General (non-symmetric) triangle wave</A>
</UL>
<BR>
<LI><A ID="tex2html3321"
HREF="node193.html">Predicting and controlling foldover</A>
<UL>
<LI><A ID="tex2html3322"
HREF="node194.html">Over-sampling</A>
<LI><A ID="tex2html3323"
HREF="node195.html">Sneaky triangle waves</A>
<LI><A ID="tex2html3324"
HREF="node196.html">Transition splicing</A>
</UL>
<BR>
<LI><A ID="tex2html3325"
HREF="node197.html">Examples</A>
<UL>
<LI><A ID="tex2html3326"
HREF="node198.html">Combining sawtooth waves</A>
<LI><A ID="tex2html3327"
HREF="node199.html">Strategies for band-limiting sawtooth waves</A>
</UL>
<BR>
<LI><A ID="tex2html3328"
HREF="node200.html">Exercises</A>
</UL>
<!--End of Table of Child-Links-->
<HR>
<!--Navigation Panel-->
<A ID="tex2html3311"
HREF="node185.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A ID="tex2html3305"
HREF="book.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A ID="tex2html3299"
HREF="node183.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A ID="tex2html3307"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A ID="tex2html3309"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A ID="tex2html3312"
HREF="node185.html">Symmetries and Fourier series</A>
<B> Up:</B> <A ID="tex2html3306"
HREF="book.html">book</A>
<B> Previous:</B> <A ID="tex2html3300"
HREF="node183.html">Exercises</A>
<B> <A ID="tex2html3308"
HREF="node4.html">Contents</A></B>
<B> <A ID="tex2html3310"
HREF="node201.html">Index</A></B>
<!--End of Navigation Panel-->
<ADDRESS>
Miller Puckette
2006-12-30
</ADDRESS>
</BODY>
</HTML>