<!DOCTYPE html>
<!--Converted with LaTeX2HTML 2002-2-1 (1.71)
original version by: Nikos Drakos, CBLU, University of Leeds
* revised and updated by: Marcus Hennecke, Ross Moore, Herb Swan
* with significant contributions from:
Jens Lippmann, Marek Rouchal, Martin Wilck and others -->
<HTML>
<HEAD>
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<TITLE>Stretching the unit circle with rational functions</TITLE>
<META NAME="description" CONTENT="Stretching the unit circle with rational functions">
<META NAME="keywords" CONTENT="book">
<META NAME="resource-type" CONTENT="document">
<META NAME="distribution" CONTENT="global">
<META NAME="Generator" CONTENT="LaTeX2HTML v2002-2-1">
<META HTTP-EQUIV="Content-Style-Type" CONTENT="text/css">
<LINK REL="STYLESHEET" HREF="book.css">
<LINK REL="next" HREF="node147.html">
<LINK REL="previous" HREF="node145.html">
<LINK REL="up" HREF="node139.html">
<LINK REL="next" HREF="node147.html">
</HEAD>
<BODY >
<!--Navigation Panel-->
<A ID="tex2html2758"
HREF="node147.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A ID="tex2html2752"
HREF="node139.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A ID="tex2html2746"
HREF="node145.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A ID="tex2html2754"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A ID="tex2html2756"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A ID="tex2html2759"
HREF="node147.html">Butterworth band-pass filter</A>
<B> Up:</B> <A ID="tex2html2753"
HREF="node139.html">Designing filters</A>
<B> Previous:</B> <A ID="tex2html2747"
HREF="node145.html">Butterworth filters</A>
<B> <A ID="tex2html2755"
HREF="node4.html">Contents</A></B>
<B> <A ID="tex2html2757"
HREF="node201.html">Index</A></B>
<BR>
<BR>
<!--End of Navigation Panel-->
<H2><A ID="SECTION001237000000000000000">
Stretching the unit circle with rational functions</A>
</H2>
<P>
In Section <A HREF="node143.html#sect8.twopolebandpass">8.3.4</A> we saw a simple way to turn a low-pass
filter into a band-pass one. It is tempting to apply the same method to turn
our Butterworth low-pass filter into a higher-quality band-pass filter; but if
we wish to preserve the high quality of the Butterworth filter we must be more
careful than before in the design of the transformation used. In this section
we will prepare the way to making the Butterworth band-pass filter by
introducing a class of rational transformations of the complex plane which
preserve the unit circle.
<P>
This discussion is adapted from [<A
HREF="node202.html#r-parks87">PB87</A>], pp. 201-206 (I'm grateful
to Julius Smith for this pointer). There the transformation is carried out
in continuous time, but here we have adapted the method to operate in
discrete time, in order to make the discussion self-contained.
<P>
The idea is to start with any filter with a transfer function as before:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H(Z) = {
{
(1 - {Q_1}{Z^{-1}}) \cdots (1 - {Q_j}{Z^{-1}})
} \over {
(1 - {P_1}{Z^{-1}}) \cdots (1 - {P_k}{Z^{-1}})
}
}
\end{displaymath}
-->
<IMG
WIDTH="263" HEIGHT="45" BORDER="0"
SRC="img889.png"
ALT="\begin{displaymath}
H(Z) = {
{
(1 - {Q_1}{Z^{-1}}) \cdots (1 - {Q_j}{Z^{-1}})
} \over {
(1 - {P_1}{Z^{-1}}) \cdots (1 - {P_k}{Z^{-1}})
}
}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
whose frequency response (the gain at a frequency <IMG
WIDTH="14" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img27.png"
ALT="$\omega $">) is given by:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
| H(\cos(\omega) + i \sin(\omega)) |
\end{displaymath}
-->
<IMG
WIDTH="146" HEIGHT="28" BORDER="0"
SRC="img938.png"
ALT="\begin{displaymath}
\vert H(\cos(\omega) + i \sin(\omega)) \vert
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<P>
Now suppose we can find a rational function, <IMG
WIDTH="40" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img939.png"
ALT="$R(Z)$">, which distorts the
unit circle in some desirable way. For <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> to be a rational function means
that it can be written as a quotient of two polynomials (for example, the
transfer function <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> is a rational function). That <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> sends points on the
unit circle to other points on the unit circle is just the condition that
<IMG
WIDTH="78" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img940.png"
ALT="$\vert R(Z)\vert = 1$"> whenever <IMG
WIDTH="44" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img941.png"
ALT="$Z=1$">. It can easily be checked that any function of
the form
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
R(Z) = U \cdot
{{
{A_n}{Z^n} + {A_{n-1}}{Z^{n-1}} + \cdots + {A_0}
} \over {
\overline{A_0}{Z^n} + \overline{A_1}{Z^{n-1}} + \cdots + \overline{A_n}
}}
\end{displaymath}
-->
<IMG
WIDTH="295" HEIGHT="45" BORDER="0"
SRC="img942.png"
ALT="\begin{displaymath}
R(Z) = U \cdot
{{
{A_n}{Z^n} + {A_{n-1}}{Z^{n-1}} + \cdot...
...}{Z^n} + \overline{A_1}{Z^{n-1}} + \cdots + \overline{A_n}
}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
(where <IMG
WIDTH="54" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img943.png"
ALT="$\vert U\vert=1$">) has this property. The same reasoning as in Section
<A HREF="node134.html#sect8.secondform">8.2.2</A> confirms that <IMG
WIDTH="78" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img940.png"
ALT="$\vert R(Z)\vert = 1$"> whenever <IMG
WIDTH="44" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img941.png"
ALT="$Z=1$">.
<P>
Once we have a suitable rational function <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$">, we can simply compose it with the
original transfer function <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> to fabricate a new rational function,
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
J(Z) = H(R(Z))
\end{displaymath}
-->
<IMG
WIDTH="117" HEIGHT="28" BORDER="0"
SRC="img944.png"
ALT="\begin{displaymath}
J(Z) = H(R(Z))
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
The gain of the new filter <IMG
WIDTH="13" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img945.png"
ALT="$J$"> at the frequency <IMG
WIDTH="14" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img27.png"
ALT="$\omega $"> is then equal to
that of <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> at a different frequency <IMG
WIDTH="13" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img77.png"
ALT="$\phi$">, chosen so that:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
\cos(\phi) + i \sin(\phi) = R(\cos(\omega) + i \sin(\omega))
\end{displaymath}
-->
<IMG
WIDTH="270" HEIGHT="28" BORDER="0"
SRC="img946.png"
ALT="\begin{displaymath}
\cos(\phi) + i \sin(\phi) = R(\cos(\omega) + i \sin(\omega))
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
The function <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> moves points around on the unit
circle; <IMG
WIDTH="13" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img945.png"
ALT="$J$"> at any point equals <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> on the point <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> moves it to.
<P>
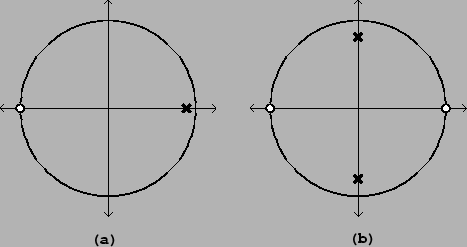
For example, suppose we start with a one-zero, one-pole low-pass filter:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H(Z) =
{{
1 + {Z^{-1}}
} \over {
1 - g{Z^{-1}}
}}
\end{displaymath}
-->
<IMG
WIDTH="127" HEIGHT="44" BORDER="0"
SRC="img947.png"
ALT="\begin{displaymath}
H(Z) =
{{
1 + {Z^{-1}}
} \over {
1 - g{Z^{-1}}
}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
and apply the function
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
R(Z) = -{Z^2} = -
{{
1 \cdot {Z^2} + 0 \cdot Z + 0
} \over {
0 \cdot {Z^2} + 0 \cdot Z + 1
}}
\end{displaymath}
-->
<IMG
WIDTH="242" HEIGHT="42" BORDER="0"
SRC="img948.png"
ALT="\begin{displaymath}
R(Z) = -{Z^2} = -
{{
1 \cdot {Z^2} + 0 \cdot Z + 0
} \over {
0 \cdot {Z^2} + 0 \cdot Z + 1
}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
Geometrically, this choice of <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> stretches the unit circle uniformly to twice
its circumference and wraps it around itself twice. The points <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img262.png"
ALT="$1$"> and
<IMG
WIDTH="23" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img401.png"
ALT="$-1$"> are both sent to the point <IMG
WIDTH="23" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img401.png"
ALT="$-1$">, and the points <IMG
WIDTH="9" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img646.png"
ALT="$i$"> and <IMG
WIDTH="21" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img949.png"
ALT="$-i$"> are sent
to the point <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img262.png"
ALT="$1$">. The resulting transfer
function is
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
J(Z) =
{{
1 - {Z^{-2}}
} \over {
1 + g{Z^{-2}}
}}
=
{{
(1 - {Z^{-1}})(1 + {Z^{-1}})
} \over {
(1 - i\sqrt{g} {Z^{-1}})(1 + i\sqrt{g} {Z^{-1}})
}}
\end{displaymath}
-->
<IMG
WIDTH="339" HEIGHT="46" BORDER="0"
SRC="img950.png"
ALT="\begin{displaymath}
J(Z) =
{{
1 - {Z^{-2}}
} \over {
1 + g{Z^{-2}}
}}
=
...
... \over {
(1 - i\sqrt{g} {Z^{-1}})(1 + i\sqrt{g} {Z^{-1}})
}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
The pole-zero plots of <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> and <IMG
WIDTH="13" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img945.png"
ALT="$J$"> are shown in Figure <A HREF="#fig08.19">8.19</A>. From
a low-pass filter we ended up with a band-pass filter. The points <IMG
WIDTH="9" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img646.png"
ALT="$i$"> and <IMG
WIDTH="21" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img949.png"
ALT="$-i$">
which <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> sends to <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img262.png"
ALT="$1$"> (where the original filter's gain is highest) become
points of highest gain for the new filter.
<P>
<DIV ALIGN="CENTER"><A ID="fig08.19"></A><A ID="10765"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 8.19:</STRONG>
One-pole, one-zero low-pass filter: (a) pole-zero plot; (b)
plot for the resulting filter after the transformation <IMG
WIDTH="92" HEIGHT="34" ALIGN="MIDDLE" BORDER="0"
SRC="img51.png"
ALT="$R(Z) = -{Z^2}$">. The
result is a band-pass filter with center frequency <IMG
WIDTH="29" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img5.png"
ALT="$\pi /2$">.
</CAPTION>
<TR><TD><IMG
WIDTH="467" HEIGHT="247" BORDER="0"
SRC="img951.png"
ALT="\begin{figure}\psfig{file=figs/fig08.19.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
<HR>
<!--Navigation Panel-->
<A ID="tex2html2758"
HREF="node147.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A ID="tex2html2752"
HREF="node139.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A ID="tex2html2746"
HREF="node145.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A ID="tex2html2754"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A ID="tex2html2756"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A ID="tex2html2759"
HREF="node147.html">Butterworth band-pass filter</A>
<B> Up:</B> <A ID="tex2html2753"
HREF="node139.html">Designing filters</A>
<B> Previous:</B> <A ID="tex2html2747"
HREF="node145.html">Butterworth filters</A>
<B> <A ID="tex2html2755"
HREF="node4.html">Contents</A></B>
<B> <A ID="tex2html2757"
HREF="node201.html">Index</A></B>
<!--End of Navigation Panel-->
<ADDRESS>
Miller Puckette
2006-12-30
</ADDRESS>
</BODY>
</HTML>