<!DOCTYPE html>
<!--Converted with LaTeX2HTML 2002-2-1 (1.71)
original version by: Nikos Drakos, CBLU, University of Leeds
* revised and updated by: Marcus Hennecke, Ross Moore, Herb Swan
* with significant contributions from:
Jens Lippmann, Marek Rouchal, Martin Wilck and others -->
<HTML>
<HEAD>
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<TITLE>The sampling theorem</TITLE>
<META NAME="description" CONTENT="The sampling theorem">
<META NAME="keywords" CONTENT="book">
<META NAME="resource-type" CONTENT="document">
<META NAME="distribution" CONTENT="global">
<META NAME="Generator" CONTENT="LaTeX2HTML v2002-2-1">
<META HTTP-EQUIV="Content-Style-Type" CONTENT="text/css">
<LINK REL="STYLESHEET" HREF="book.css">
<LINK REL="next" HREF="node42.html">
<LINK REL="previous" HREF="node40.html">
<LINK REL="up" HREF="node40.html">
<LINK REL="next" HREF="node42.html">
</HEAD>
<BODY >
<!--Navigation Panel-->
<A NAME="tex2html1161"
HREF="node42.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A NAME="tex2html1155"
HREF="node40.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A NAME="tex2html1149"
HREF="node40.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A NAME="tex2html1157"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A NAME="tex2html1159"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html1162"
HREF="node42.html">Control</A>
<B> Up:</B> <A NAME="tex2html1156"
HREF="node40.html">Audio and control computations</A>
<B> Previous:</B> <A NAME="tex2html1150"
HREF="node40.html">Audio and control computations</A>
<B> <A NAME="tex2html1158"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html1160"
HREF="node201.html">Index</A></B>
<BR>
<BR>
<!--End of Navigation Panel-->
<H1><A NAME="SECTION00710000000000000000"></A>
<A NAME="sect3.sampling"></A>
<BR>
The sampling theorem
</H1>
<P>
So far we have discussed digital audio signals as if they were capable of
describing any function of time, in the sense that knowing the values the
function takes on the integers should somehow determine the values it takes
between them. This isn't really true. For instance, suppose some function
<IMG
WIDTH="13" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img112.png"
ALT="$f$"> (defined for real numbers) happens to attain the value 1 at all integers:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
f(n) = 1 \, , \, \, \, \, \, n = \, \, \ldots, -1, 0, 1, \ldots
\end{displaymath}
-->
<IMG
WIDTH="221" HEIGHT="28" BORDER="0"
SRC="img298.png"
ALT="\begin{displaymath}
f(n) = 1 \, , \, \, \, \, \, n = \, \, \ldots, -1, 0, 1, \ldots
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
We might guess that <IMG
WIDTH="60" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img299.png"
ALT="$f(t)=1$"> for all real <IMG
WIDTH="9" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img82.png"
ALT="$t$">. But perhaps <IMG
WIDTH="13" HEIGHT="30" ALIGN="MIDDLE" BORDER="0"
SRC="img112.png"
ALT="$f$"> happens
to be one for integers and zero everywhere else--that's a perfectly
good function too, and nothing about the function's values at the integers
distinguishes it from the simpler <IMG
WIDTH="60" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img299.png"
ALT="$f(t)=1$">. But intuition tells us that
the constant function is in the <I>spirit</I> of digital audio signals,
whereas the one that hides a secret between the samples isn't. A function
that is ``possible to sample" should be one for which we can use some reasonable
interpolation scheme to deduce its values on non-integers from its values on
integers.
<P>
It is customary at this point in discussions of computer music to invoke
the famous
<A NAME="3554"></A><I>Nyquist theorem</I>.
This states (roughly speaking) that if a function is a finite or even infinite
combination of sinusoids, none of whose angular frequencies exceeds <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">,
then, theoretically at least, it is fully determined by the function's values
on the integers. One possible way of reconstructing the function would be
as a limit of higher- and higher-order polynomial interpolation.
<P>
The angular frequency <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">, called the <I>Nyquist frequency</I>, corresponds
to <IMG
WIDTH="31" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img300.png"
ALT="$R/2$"> cycles per second if <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img36.png"
ALT="$R$"> is the sample rate. The corresponding period
is two samples. The Nyquist frequency is the best we can do in the sense that
any real sinusoid of higher frequency is equal, at the integers, to one whose
frequency is lower than the Nyquist, and it is this lower frequency that will
get reconstructed by the ideal interpolation process. For instance, a
sinusoid with angular frequency between <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $"> and <IMG
WIDTH="21" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img16.png"
ALT="$2\pi $">, say <IMG
WIDTH="43" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img301.png"
ALT="$\pi + \omega$">,
can be written as
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
\cos((\pi + \omega)n + \phi) = \cos((\pi + \omega)n + \phi - 2\pi n)
\end{displaymath}
-->
<IMG
WIDTH="314" HEIGHT="28" BORDER="0"
SRC="img302.png"
ALT="\begin{displaymath}
\cos((\pi + \omega)n + \phi) = \cos((\pi + \omega)n + \phi - 2\pi n)
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
= \cos((\omega - \pi)n + \phi)
\end{displaymath}
-->
<IMG
WIDTH="139" HEIGHT="28" BORDER="0"
SRC="img303.png"
ALT="\begin{displaymath}
= \cos((\omega - \pi)n + \phi)
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
= \cos((\pi - \omega)n - \phi)
\end{displaymath}
-->
<IMG
WIDTH="139" HEIGHT="28" BORDER="0"
SRC="img304.png"
ALT="\begin{displaymath}
= \cos((\pi - \omega)n - \phi)
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
for all integers <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img75.png"
ALT="$n$">. (If <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img75.png"
ALT="$n$"> weren't an integer the first step would fail.)
So a sinusoid with frequency between <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $"> and <IMG
WIDTH="21" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img16.png"
ALT="$2\pi $"> is equal, on the
integers at least, to one with frequency between 0 and <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">; you simply can't
tell the two apart. And since any conversion hardware should do the ``right"
thing and reconstruct the lower-frequency sinusoid, any higher-frequency one
you try to synthesize will come out your speakers at the wrong
frequency--specifically, you will hear the unique frequency between 0 and <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">
that the higher frequency lands on when reduced in the above way. This
phenomenon is called
<I>foldover</I>,
<A NAME="3558"></A>
because the half-line of frequencies from 0
to <IMG
WIDTH="19" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img305.png"
ALT="$\infty$"> is folded back and forth, in lengths of <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">, onto the interval
from 0 to <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">. The word
<I>aliasing</I>
<A NAME="3560"></A>means the same thing. Figure <A HREF="#fig03.01">3.1</A> shows that sinusoids of angular
frequencies <IMG
WIDTH="29" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img5.png"
ALT="$\pi /2$"> and <IMG
WIDTH="37" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img6.png"
ALT="$3\pi /2$">, for instance, can't be distinguished
as digital audio signals.
<P>
<DIV ALIGN="CENTER"><A NAME="fig03.01"></A><A NAME="3564"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 3.1:</STRONG>
Two real sinusoids, with angular frequencies <IMG
WIDTH="29" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img5.png"
ALT="$\pi /2$"> and <IMG
WIDTH="37" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img6.png"
ALT="$3\pi /2$">,
showing that they coincide at integers. A digital audio signal can't
distinguish between the two.</CAPTION>
<TR><TD><IMG
WIDTH="311" HEIGHT="110" BORDER="0"
SRC="img306.png"
ALT="\begin{figure}\psfig{file=figs/fig03.01.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
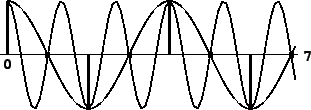We conclude that when, for instance, we're computing values of a
Fourier series (Page <A HREF="node14.html#eq-fourierseries"><IMG ALIGN="BOTTOM" BORDER="1" ALT="[*]"
SRC="crossref.png"></A>),
either as a wavetable or as a real-time signal, we had better leave out any
sinusoid
in the sum whose frequency exceeds <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $">. But the picture in general is not
this simple, since most techniques other than additive synthesis don't lead to
neat, band-limited signals (ones whose components stop at some limited
frequency). For example, a sawtooth wave of frequency <IMG
WIDTH="14" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img27.png"
ALT="$\omega $">, of the form
put out by Pd's <TT>phasor~</TT> object but considered as a continuous
function <IMG
WIDTH="31" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img307.png"
ALT="$f(t)$">, expands to:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
f(t) = {1 \over 2} - {1 \over \pi}
{ \left (
\sin(\omega t) + {{\sin(2 \omega t)} \over 2} +
{{\sin(3 \omega t)} \over 3} + \cdots
\right ) }
\end{displaymath}
-->
<IMG
WIDTH="357" HEIGHT="45" BORDER="0"
SRC="img308.png"
ALT="\begin{displaymath}
f(t) = {1 \over 2} - {1 \over \pi}
{ \left (
\sin(\omega ...
...\over 2} +
{{\sin(3 \omega t)} \over 3} + \cdots
\right ) }
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
which enjoys arbitrarily high frequencies; and moreover the hundredth partial
is only 40 dB weaker than the first one. At any but very low values of
<IMG
WIDTH="14" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img27.png"
ALT="$\omega $">, the partials above <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $"> will be audibly present--and, because of
foldover, they will be heard at incorrect frequencies. (This does not mean
that one shouldn't use sawtooth waves as phase generators--the wavetable
lookup step magically corrects the sawtooth's foldover--but one should think
twice before using a sawtooth wave itself as a digital sound source.)
<P>
Many synthesis techniques, even if not strictly band-limited, give partials
which may be made to drop off more rapidly than <IMG
WIDTH="28" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img309.png"
ALT="$1/n$"> as in the sawtooth
example, and are thus more forgiving to work with digitally. In any case,
it is always a good idea to keep the possibility of foldover in mind, and
to train your ears to recognize it.
<P>
The first line of defense against foldover is simply to use high sample rates;
it is a good practice to systematically use the highest sample rate that your
computer can easily handle. The highest practical rate will vary according to
whether you are working in real time or not, CPU time and memory constraints,
and/or input and output hardware, and sometimes even software-imposed
limitations.
<P>
A very non-technical treatment of sampling theory is given in
[<A
HREF="node202.html#r-ballora03">Bal03</A>]. More detail can be found in [<A
HREF="node202.html#r-mathews69">Mat69</A>, pp. 1-30].
<P>
<HR>
<!--Navigation Panel-->
<A NAME="tex2html1161"
HREF="node42.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A NAME="tex2html1155"
HREF="node40.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A NAME="tex2html1149"
HREF="node40.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A NAME="tex2html1157"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A NAME="tex2html1159"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html1162"
HREF="node42.html">Control</A>
<B> Up:</B> <A NAME="tex2html1156"
HREF="node40.html">Audio and control computations</A>
<B> Previous:</B> <A NAME="tex2html1150"
HREF="node40.html">Audio and control computations</A>
<B> <A NAME="tex2html1158"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html1160"
HREF="node201.html">Index</A></B>
<!--End of Navigation Panel-->
<ADDRESS>
Miller Puckette
2006-12-30
</ADDRESS>
</BODY>
</HTML>