<!DOCTYPE html>
<!--Converted with LaTeX2HTML 2002-2-1 (1.71)
original version by: Nikos Drakos, CBLU, University of Leeds
* revised and updated by: Marcus Hennecke, Ross Moore, Herb Swan
* with significant contributions from:
Jens Lippmann, Marek Rouchal, Martin Wilck and others -->
<HTML>
<HEAD>
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<TITLE>Recirculating delay networks</TITLE>
<META NAME="description" CONTENT="Recirculating delay networks">
<META NAME="keywords" CONTENT="book">
<META NAME="resource-type" CONTENT="document">
<META NAME="distribution" CONTENT="global">
<META NAME="Generator" CONTENT="LaTeX2HTML v2002-2-1">
<META HTTP-EQUIV="Content-Style-Type" CONTENT="text/css">
<LINK REL="STYLESHEET" HREF="book.css">
<LINK REL="next" HREF="node110.html">
<LINK REL="previous" HREF="node108.html">
<LINK REL="up" HREF="node104.html">
<LINK REL="next" HREF="node110.html">
</HEAD>
<BODY >
<!--Navigation Panel-->
<A NAME="tex2html2185"
HREF="node110.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A NAME="tex2html2179"
HREF="node104.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A NAME="tex2html2173"
HREF="node108.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A NAME="tex2html2181"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A NAME="tex2html2183"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html2186"
HREF="node110.html">Power conservation and complex</A>
<B> Up:</B> <A NAME="tex2html2180"
HREF="node104.html">Time shifts and delays</A>
<B> Previous:</B> <A NAME="tex2html2174"
HREF="node108.html">Delay networks</A>
<B> <A NAME="tex2html2182"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html2184"
HREF="node201.html">Index</A></B>
<BR>
<BR>
<!--End of Navigation Panel-->
<H1><A NAME="SECTION001140000000000000000"></A>
<A NAME="sect7.recirculatingcomb"></A>
<BR>
Recirculating delay networks
</H1>
<P>
It is sometimes desirable to connect the outputs of one or more delays in a
network back into their own or each others' inputs. Instead of getting one
or several echos of the original sound as in the example above, we
can potentially get an infinite number of echos, each one feeding back into
the network to engender yet others.
<P>
The simplest example of a recirculating network is the
<A NAME="7935"></A>
<I>recirculating comb filter</I>
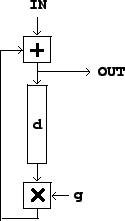
whose block diagram is shown in Figure <A HREF="#fig07.07">7.7</A>. As with the
earlier, simple comb filter, the input signal is sent down a delay line whose
length is <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img28.png"
ALT="$d$"> samples. But now the delay line's
output is also fed back to its input; the delay's input is the sum of
the original input and the delay's output. The output is
multiplied by a number <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> before feeding it back into its input.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.07"></A><A NAME="7940"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.7:</STRONG>
Block diagram for a recirculating comb filter. Here <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img28.png"
ALT="$d$"> is the
delay time in samples and <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> is the feedback coefficient.</CAPTION>
<TR><TD><IMG
WIDTH="125" HEIGHT="221" BORDER="0"
SRC="img708.png"
ALT="\begin{figure}\psfig{file=figs/fig07.07.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
The time domain behavior of the recirculating comb filter is shown in Figure
<A HREF="#fig07.08">7.8</A>. Here we consider the effect of sending an impulse into the
network. We get back the original impulse, plus a series of echos, each
in turn <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img28.png"
ALT="$d$"> samples after the previous one, and multiplied each time by the
gain <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$">. In general, a delay network's output given an impulse as input is
called the network's
<A NAME="7944"></A><I>impulse response</I>.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.08"></A><A NAME="7948"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.8:</STRONG>
Time-domain analysis of the recirculating comb filter, using
an impulse as input.</CAPTION>
<TR><TD><IMG
WIDTH="440" HEIGHT="257" BORDER="0"
SRC="img709.png"
ALT="\begin{figure}\psfig{file=figs/fig07.08.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
Note that we have chosen a gain <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> that is less than one in absolute value.
If we chose a gain greater than one (or less than -1), each echo would have
a larger magnitude than the previous one. Instead of falling exponentially
as they do in the figure, they would grow exponentially. A recirculating
network whose output eventually falls toward zero after its input terminates
is called
<A NAME="7951"></A><I>stable</I>;
one whose output grows without bound is called <I>unstable</I>.
<P>
We can also analyse the recirculating comb filter in the frequency domain.
The situation is now quite
hard to analyze using real sinusoids, and so we get the first big payoff
for having introduced complex numbers, which greatly simplify the analysis.
<P>
If, as before, we feed the input with the signal,
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
X[n] = Z^n
\end{displaymath}
-->
<IMG
WIDTH="74" HEIGHT="28" BORDER="0"
SRC="img710.png"
ALT="\begin{displaymath}
X[n] = Z^n
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
with <IMG
WIDTH="53" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img22.png"
ALT="$\vert Z\vert=1$">, we can write the output as
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
Y[n] = (1 + g{Z^{-d}} + {g^2}{Z^{-2d}} + \cdots) X[n]
\end{displaymath}
-->
<IMG
WIDTH="270" HEIGHT="28" BORDER="0"
SRC="img711.png"
ALT="\begin{displaymath}
Y[n] = (1 + g{Z^{-d}} + {g^2}{Z^{-2d}} + \cdots) X[n]
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
Here the terms in the sum come from the series of
discrete echos.
It follows that the amplitude of the output is:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H = 1 + g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + \cdots
\end{displaymath}
-->
<IMG
WIDTH="214" HEIGHT="28" BORDER="0"
SRC="img712.png"
ALT="\begin{displaymath}
H = 1 + g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + \cdots
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
This is a geometric series; we can sum it using the standard technique. First
multiply both sides by <IMG
WIDTH="41" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img713.png"
ALT="$g{Z^{-d}}$"> to give:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
g{Z^{-d}} H = g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + {(g{Z^{-d}})} ^ 3 + \cdots
\end{displaymath}
-->
<IMG
WIDTH="300" HEIGHT="28" BORDER="0"
SRC="img714.png"
ALT="\begin{displaymath}
g{Z^{-d}} H = g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + {(g{Z^{-d}})} ^ 3 + \cdots
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
and subtract from the original equation to give:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H - g{Z^{-d}} H = 1
\end{displaymath}
-->
<IMG
WIDTH="115" HEIGHT="27" BORDER="0"
SRC="img715.png"
ALT="\begin{displaymath}
H - g{Z^{-d}} H = 1
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
Then solve for <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$">:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H = {1 \over {1 - g{Z^{-d}}}}
\end{displaymath}
-->
<IMG
WIDTH="102" HEIGHT="41" BORDER="0"
SRC="img716.png"
ALT="\begin{displaymath}
H = {1 \over {1 - g{Z^{-d}}}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<P>
A faster (but slightly less intuitive) method to get the same result is to
examine the recirculating network itself to yield an equation for <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$">, as
follows. We named the input <IMG
WIDTH="36" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img669.png"
ALT="$X[n]$"> and the output <IMG
WIDTH="34" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img717.png"
ALT="$Y[n]$">. The signal going
into the delay line is the output <IMG
WIDTH="34" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img717.png"
ALT="$Y[n]$">, and passing this through the delay
line and multiplier gives
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
Y[n] \cdot g{Z^{-d}}
\end{displaymath}
-->
<IMG
WIDTH="79" HEIGHT="28" BORDER="0"
SRC="img718.png"
ALT="\begin{displaymath}
Y[n] \cdot g{Z^{-d}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
This plus the input is just the output signal again, so:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
Y[n] = X[n]+Y[n] \cdot g{Z^{-d}}
\end{displaymath}
-->
<IMG
WIDTH="185" HEIGHT="28" BORDER="0"
SRC="img719.png"
ALT="\begin{displaymath}
Y[n] = X[n]+Y[n] \cdot g{Z^{-d}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
and dividing by <IMG
WIDTH="36" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img669.png"
ALT="$X[n]$"> and using <IMG
WIDTH="111" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img720.png"
ALT="$H=Y[n]/X[n]$"> gives:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
H = 1 + Hg{Z^{-d}}
\end{displaymath}
-->
<IMG
WIDTH="115" HEIGHT="27" BORDER="0"
SRC="img721.png"
ALT="\begin{displaymath}
H = 1 + Hg{Z^{-d}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
This is equivalent to the earlier equation for <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$">.
<P>
Now we would like to make a graph of the frequency response (the gain as a
function of frequency) as
we did for non-recirculating comb filters in
Figure <A HREF="node108.html#fig07.06">7.6</A>. This
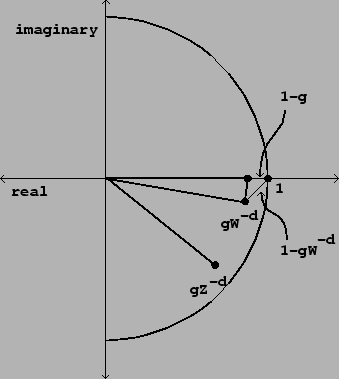
again requires that we make a preliminary picture in the complex plane. We
would like to estimate the magnitude of <IMG
WIDTH="18" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img25.png"
ALT="$H$"> equal to:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
|H| = {1 \over {|1 - g{Z^{-d}}|}}
\end{displaymath}
-->
<IMG
WIDTH="118" HEIGHT="42" BORDER="0"
SRC="img722.png"
ALT="\begin{displaymath}
\vert H\vert = {1 \over {\vert 1 - g{Z^{-d}}\vert}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
where we used the multiplicative property of magnitudes to conclude that the
magnitude of a (complex) reciprocal is the reciprocal of a (real) magnitude.
Figure <A HREF="#fig07.09">7.9</A> shows the situation graphically. The gain <IMG
WIDTH="26" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img30.png"
ALT="$\vert H\vert$"> is
the reciprocal of the length of the segment reaching from the point 1 to the
point <IMG
WIDTH="41" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img713.png"
ALT="$g{Z^{-d}}$">. Figure
<A HREF="#fig07.10">7.10</A> shows a graph of the
frequency response <IMG
WIDTH="26" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img30.png"
ALT="$\vert H\vert$"> as a function of the angular frequency
<!-- MATH
$\omega = \angle(Z)$
-->
<IMG
WIDTH="69" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img678.png"
ALT="$\omega = \angle(Z)$">.
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.09"></A><A NAME="7976"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.9:</STRONG>
Diagram in the complex plane for approximating the output gain <IMG
WIDTH="26" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img30.png"
ALT="$\vert H\vert$">
of the
recirculating comb filters at three different frequencies: 0, and the
arguments of two unit complex numbers <IMG
WIDTH="20" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img31.png"
ALT="$W$"> and <IMG
WIDTH="15" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img20.png"
ALT="$Z$">; <IMG
WIDTH="20" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img31.png"
ALT="$W$">
is chosen to give a gain about 3 dB below the peak.</CAPTION>
<TR><TD><IMG
WIDTH="339" HEIGHT="379" BORDER="0"
SRC="img723.png"
ALT="\begin{figure}\psfig{file=figs/fig07.09.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
<DIV ALIGN="CENTER"><A NAME="fig07.10"></A><A NAME="7981"></A>
<TABLE>
<CAPTION ALIGN="BOTTOM"><STRONG>Figure 7.10:</STRONG>
Frequency response of the recirculating comb filter with <IMG
WIDTH="53" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img32.png"
ALT="$g = 0.8$">.
The peak
gain is <IMG
WIDTH="67" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img33.png"
ALT="$1/(1-g)$"> = 5. Peaks are much narrower than for the non-recirculating
comb filter.</CAPTION>
<TR><TD><IMG
WIDTH="312" HEIGHT="148" BORDER="0"
SRC="img724.png"
ALT="\begin{figure}\psfig{file=figs/fig07.10.ps}\end{figure}"></TD></TR>
</TABLE>
</DIV>
<P>
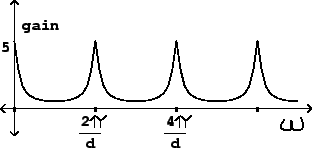Figure <A HREF="#fig07.09">7.9</A> can be used to analyze how the frequency response
<IMG
WIDTH="49" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img725.png"
ALT="$\vert H(\omega)\vert$"> should
behave
qualitatively as a function of <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$">. The height and bandwidth of the peaks
both depend on <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$">. The maximum value that <IMG
WIDTH="26" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img30.png"
ALT="$\vert H\vert$"> can attain is
when
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
{Z^{-d}} = 1
\end{displaymath}
-->
<IMG
WIDTH="56" HEIGHT="24" BORDER="0"
SRC="img726.png"
ALT="\begin{displaymath}
{Z^{-d}} = 1
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
This occurs at the frequencies <!-- MATH
$\omega = 0, 2\pi/d , 4\pi/d , \ldots$
-->
<IMG
WIDTH="150" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img727.png"
ALT="$\omega = 0, 2\pi/d , 4\pi/d , \ldots$"> as in the
simple comb filter above. At these frequencies the gain reaches
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
|H| = {1 \over {1 - g}}
\end{displaymath}
-->
<IMG
WIDTH="80" HEIGHT="41" BORDER="0"
SRC="img728.png"
ALT="\begin{displaymath}
\vert H\vert = {1 \over {1 - g}}
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
<P>
The next important question is the bandwidth of the peaks in the frequency
response. So we would like to find sinusoids <IMG
WIDTH="29" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img729.png"
ALT="$W^n$">, with frequency
<IMG
WIDTH="43" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img730.png"
ALT="$\angle(W)$">, giving rise to a value of <IMG
WIDTH="26" HEIGHT="32" ALIGN="MIDDLE" BORDER="0"
SRC="img30.png"
ALT="$\vert H\vert$"> that is, say, 3 decibels below the
maximum. To do this, we return to Figure <A HREF="#fig07.09">7.9</A>, and try to place <IMG
WIDTH="20" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img31.png"
ALT="$W$">
so that the distance from the point 1 to the point <IMG
WIDTH="46" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img731.png"
ALT="$gW^{-d}$"> is about
<IMG
WIDTH="24" HEIGHT="37" ALIGN="MIDDLE" BORDER="0"
SRC="img732.png"
ALT="$\sqrt{2}$"> times the distance from 1 to <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> (since <IMG
WIDTH="24" HEIGHT="37" ALIGN="MIDDLE" BORDER="0"
SRC="img732.png"
ALT="$\sqrt{2}$">:1 is a ratio of
approximately 3 decibels).
<P>
We do this by arranging for the imaginary part of
<IMG
WIDTH="46" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img731.png"
ALT="$gW^{-d}$"> to be roughly <IMG
WIDTH="39" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img733.png"
ALT="$1-g$"> or its negative, making a nearly isosceles right
triangle between the points 1, <IMG
WIDTH="39" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img733.png"
ALT="$1-g$">, and <IMG
WIDTH="46" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img731.png"
ALT="$gW^{-d}$">. (Here we're supposing that
<IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> is at least 2/3 or so; otherwise this approximation isn't very good). The
hypotenuse of a right isosceles triangle is always <IMG
WIDTH="24" HEIGHT="37" ALIGN="MIDDLE" BORDER="0"
SRC="img732.png"
ALT="$\sqrt{2}$"> times the leg,
and so the gain drops by that factor compared to its maximum.
<P>
We now make another approximation, that the imaginary part of <IMG
WIDTH="46" HEIGHT="35" ALIGN="MIDDLE" BORDER="0"
SRC="img731.png"
ALT="$gW^{-d}$">
is approximately the angle in radians it cuts from the real axis:
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
\pm(1-g) \approx \mathrm{im}({gW^{-d}}) \approx \angle({W^{-d}})
\end{displaymath}
-->
<IMG
WIDTH="231" HEIGHT="28" BORDER="0"
SRC="img734.png"
ALT="\begin{displaymath}
\pm(1-g) \approx \mathrm{im}({gW^{-d}}) \approx \angle({W^{-d}})
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
So the region of each peak reaching within 3 decibels of the maximum value
is about
<BR><P></P>
<DIV ALIGN="CENTER">
<!-- MATH
\begin{displaymath}
(1-g)/d
\end{displaymath}
-->
<IMG
WIDTH="63" HEIGHT="28" BORDER="0"
SRC="img735.png"
ALT="\begin{displaymath}
(1-g)/d
\end{displaymath}">
</DIV>
<BR CLEAR="ALL">
<P></P>
(in radians) to either side of the peak. The bandwidth narrows (and the filter
peaks become sharper) as <IMG
WIDTH="11" HEIGHT="29" ALIGN="MIDDLE" BORDER="0"
SRC="img29.png"
ALT="$g$"> approaches its maximum value of <IMG
WIDTH="11" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img262.png"
ALT="$1$">.
<P>
As with the non-recirculating comb filter of Section <A HREF="node108.html#sect7.network">7.3</A>, the
teeth of the comb are closer together for larger values of the delay <IMG
WIDTH="11" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img28.png"
ALT="$d$">. On
the other hand, a delay of <IMG
WIDTH="40" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img736.png"
ALT="$d=1$"> (the shortest possible) gets only one tooth
(at zero frequency) below the Nyquist frequency <IMG
WIDTH="13" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img41.png"
ALT="$\pi $"> (the next tooth, at
<IMG
WIDTH="21" HEIGHT="13" ALIGN="BOTTOM" BORDER="0"
SRC="img16.png"
ALT="$2\pi $">, corresponds again to a frequency of zero by foldover).
So the recirculating comb filter with <IMG
WIDTH="40" HEIGHT="14" ALIGN="BOTTOM" BORDER="0"
SRC="img736.png"
ALT="$d=1$"> is just a low-pass filter.
Delay networks
with one-sample delays will be the basis for designing many other kinds of
digital
filters in Chapter <A HREF="node127.html#chapter-filter">8</A>.
<P>
<HR>
<!--Navigation Panel-->
<A NAME="tex2html2185"
HREF="node110.html">
<IMG WIDTH="37" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="next"
SRC="next.png"></A>
<A NAME="tex2html2179"
HREF="node104.html">
<IMG WIDTH="26" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="up"
SRC="up.png"></A>
<A NAME="tex2html2173"
HREF="node108.html">
<IMG WIDTH="63" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="previous"
SRC="prev.png"></A>
<A NAME="tex2html2181"
HREF="node4.html">
<IMG WIDTH="65" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="contents"
SRC="contents.png"></A>
<A NAME="tex2html2183"
HREF="node201.html">
<IMG WIDTH="43" HEIGHT="24" ALIGN="BOTTOM" BORDER="0" ALT="index"
SRC="index.png"></A>
<BR>
<B> Next:</B> <A NAME="tex2html2186"
HREF="node110.html">Power conservation and complex</A>
<B> Up:</B> <A NAME="tex2html2180"
HREF="node104.html">Time shifts and delays</A>
<B> Previous:</B> <A NAME="tex2html2174"
HREF="node108.html">Delay networks</A>
<B> <A NAME="tex2html2182"
HREF="node4.html">Contents</A></B>
<B> <A NAME="tex2html2184"
HREF="node201.html">Index</A></B>
<!--End of Navigation Panel-->
<ADDRESS>
Miller Puckette
2006-12-30
</ADDRESS>
</BODY>
</HTML>