



Next: Phase modulation and FM
Up: Examples
Previous: Waveshaping using an exponential
Contents
Index
Another interesting class of waveshaping transfer functions is the sinusoids:
which include the cosine and sine functions (got by choosing 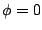 and
and
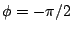 , respectively). These functions, one being even and the
other odd, give rise to even and odd harmonic spectra, which turn out to be:
, respectively). These functions, one being even and the
other odd, give rise to even and odd harmonic spectra, which turn out to be:
The functions 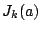 are the
Bessel functions
of the first kind, which
engineers sometimes use to solve problems about vibrations or heat flow on
discs. For other values of
are the
Bessel functions
of the first kind, which
engineers sometimes use to solve problems about vibrations or heat flow on
discs. For other values of 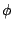 , we can expand the expression for
, we can expand the expression for 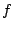 :
:
so the result is a mix between the even and the odd harmonics, with 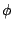 controlling the relative amplitudes of the two. This is demonstrated in Patch
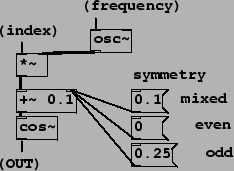
E07.evenodd.pd, shown in Figure 5.14.
controlling the relative amplitudes of the two. This is demonstrated in Patch
E07.evenodd.pd, shown in Figure 5.14.
Figure 5.14:
Using an additive offset to a cosine transfer function to alter the
symmetry between even and odd. With no offset the symmetry is even. For odd symmetry, a quarter cycle is added
to the phase. Smaller offsets give a mixture of even and odd.
 |




Next: Phase modulation and FM
Up: Examples
Previous: Waveshaping using an exponential
Contents
Index
Miller Puckette
2006-12-30
