Dissecting classical waveforms

Among the several conclusions we can draw from the even/odd harmonic decomposition of the sawtooth wave (Figure 10.2), one is that a square wave can be decomposed into a linear combination of two sawtooth waves. We can carry this idea further, and show how to compose any classical waveform having only jumps (discontinuities in value) but no corners (discontinuities in slope) as a sum of sawtooth waves of various phases and amplitudes. We then develop the idea further, showing how to generate waveforms with corners (either in addition to, or instead of, jumps) using another elementary waveform we'll call the parabolic wave.

Suppose first that a waveform of period $N$ has discontinuities at $j$ different points, ${L_1}, \ldots, {L_j}$, all lying on the cycle between 0 and $N$, at which the waveform jumps by values ${d_1}, \ldots, {d_j}$. A negative value of $d_1$, for instance, would mean that the waveform jumps from a higher to a lower value at the point ${L_1}$, and a positive value of $d_1$ would mean a jump from a lower to a higher value.

Figure 10.3: Dissecting a waveform: (a) the original waveform with two discontinuities; (b and c) the two component sawtooth waves.

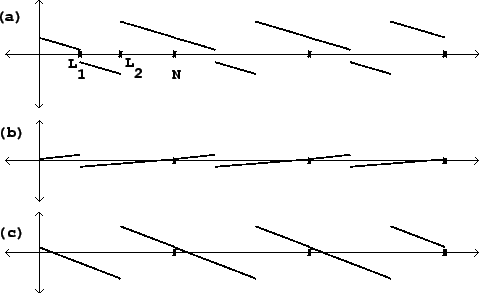For instance, Figure 10.3 (part a) shows a classical waveform with two jumps: $({L_1}, {d_1}) = (0.3N, -0.3)$ and $({L_2}, {d_2}) = (0.6N, 1.3)$. Parts (b) and (c) show sawtooth waves, each with one of the two jumps. The sum of the two sawtooth waves reconstructs the waveform of part (a), except for a possible constant (DC) offset.

The sawtooth wave with a jump of one unit at the point zero is given by

$$s[n] = n/N - 1/2$$

over the period $0 \le n \le N-1$, and repeats for other values of $n$. A sawtooth wave with a jump $(L, d)$ is given by $s'[n] = d s[n-L]$. The sum of all the component sawtooth waves is:

$$x[n] = {d_1} s[n - {L_1}] + \cdots + {d_j} s[n - {L_j}]$$

The slopes of the segments of the waveform of part (a) of the figure are all the same, equal to the sum of the slopes of the component sawtooth waves:

$$-{{{d_1} + \cdots + {d_j}} \over {N}}$$

Square and rectangle waves have horizontal line segments (slope zero); for this to happen in general the jumps must add to zero: ${d_1} + \cdots + {d_j} = 0$.

Figure 10.4: The parabolic wave.

To decompose classical waveforms with corners we use the parabolic wave, which, over a single period from 0 to $N$, is equal to

$$p[n] = {1 \over 2} {{({n\over N} - {1\over 2})}^2} - {1 \over {24}}$$

as shown in Figure 10.4. It is a second-degree (quadratic) polynomial in the variable $n$, arranged so that it reaches a maximum halfway through the cycle at $n=N/2$, the DC component is zero (or in other words, the average value over one cycle of the waveform is zero), and so that the slope changes discontinuously by $-1/N$ at the beginning of the cycle.

To construct a waveform with any desired number of corners (suppose they are at the points ${M_i}, \ldots, {M_l}$, with slope changes equal to ${c_1}, \ldots, {c_l}$), we sum up the necessary parabolic waves:

$$x[n] = {-N c_1} p[n - {M_1}] - \cdots - {N c_l} p[n - {M_l}]$$

An example is shown graphically in Figure 10.5.

Figure 10.5: Decomposing a triangle wave (part a) into two parabolic waves (b and c).

If the sum $x[n]$ is to contain line segments (not segments of curves), the $n^2$ terms in the sum must sum to zero. From the expansion of $x[n]$ above, this implies that ${c_1} + \cdots + {c_l} = 0$. Sums obtained from existing classical waveforms (as in the figure) will always satisfy this condition because the changes in slope, over a cycle, must all add to zero for the waveform to connect with itself.