Narrow-band companding: noise suppression

Figure 9.16: Noise suppression as an example of narrow-band companding: (a) analysis and reconstruction of the signal; (b) computation of the "mask".

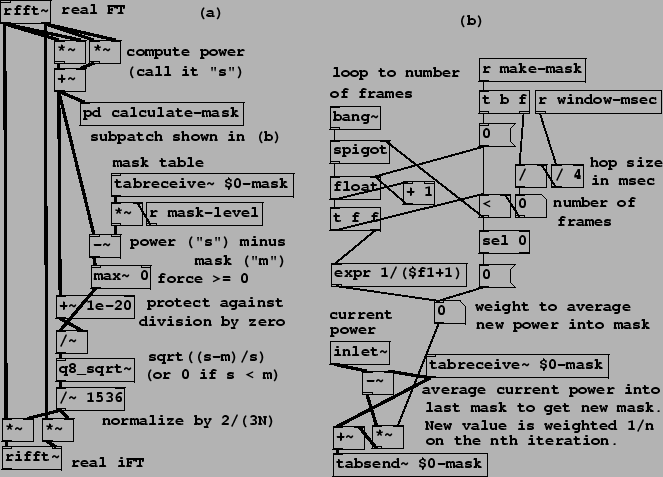
Example I04.noisegate.pd (Figure 9.16) shows an example of narrow-band companding using Fourier analysis/resynthesis. (This is a realization of the block diagram of Figure 9.8.) Part (a) of the figure shows a filter configuration similar to the previous example, except that the gain for each channel is now a function of the channel magnitude.

For each $k$, if we let $s[k]$ denote the power in channel $k$, and let $m[k]$ be a mask level (a level presumably somewhat higher than the noise power for channel $k$), then the gain in channel $k$ is given by

$$\left \{ \begin{array}{ll} {\sqrt{{s[k]-m[k]}\over {s[k]}... ... {s[k] > m[k]} \\ 0 & \mbox{otherwise} \end{array} \right .$$

The power in the $k$th channel is thus reduced by $m[k]$ if possible, and otherwise replaced by zero.

The mask itself is the product of the measured average noise in each channel, which is contained in the table "$0-mask", multiplied by a value named "mask-level". The average noise is measured in a subpatch (pd calculate-mask), whose contents are shown in part (b) of the figure. To compute the mask we are using two new new objects:

: send a bang in advance of each block of computation. The bang appears at the logical time of the first sample in each block (the earliest logical time whose control computation affects that block and not the previous one), following the scheme shown in Figure 3.2.

: the companion object for tabreceive~, repeatedly copies its input to the contents of a table, affecting up to the first $N$ samples of the table.

The power averaging process is begun by sending a time duration in milliseconds to "make-mask". The patch computes the equivalent number of blocks $b$ and generates a sequence of weights: $1, 1/2, 1/3, \ldots, 1/b$, by which each of the $b$ following blocks' power is averaged into whatever the mask table held at the previous block. At the end of $b$ blocks the table holds the equally-weighted average of all $b$ power measurements. Thereafter, the weight for averaging new power measurements is zero, so the measured average stops evolving.

To use this patch for classical noise suppression requires at least a few seconds of recorded noise without the "signal" present. This is played into the patch, and its duration sent to "make-mask", so that the "$0-mask" table holds the average measured noise power for each channel. Then, making the assumption that the noisy part of the signal rarely exceeds 10 times its average power (for example), "mask-level" is set to 10, and the signal to be noise-suppressed is sent through part (a) of the patch. The noise will be almost all gone, but those channels in which the signal exceeds 20 times the noise power will only be attenuated by 3dB, and higher-power channels progressively less. (Of course, actual noise suppression might not be the most interesting application of the patch; one could try masking any signal from any other one.)