Timbre stamping (classical vocoder)

Figure 9.9: Block diagram for timbre stamping (AKA "vocoding'').

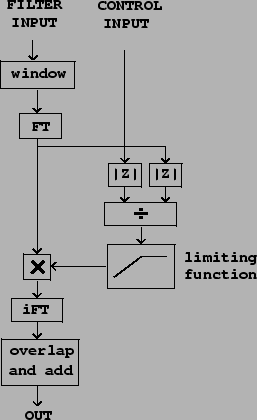
A second application of Fourier analysis and resynthesis is a time-varying filter capable of making one sound take on the evolving spectral envelope of another. This is widely known in electronic music circles as a vocoder, named, not quite accurately, after the original Bell Laboratories vocal analysis/synthesis device. The technique described here is more accurately called timbre stamping. Two input signals are used, one to be filtered, and the other to control the filter via its time-varying spectral envelope. The windowed Fourier transform is used both on the control signal input to estimate its spectral envelope, and on the filter input in order to apply the filter.

A block diagram for timbre stamping is shown in Figure 9.9. As in the previous example, the timbre stamp acts by multiplying the complex-valued windowed Fourier transform of the filter input by non-negative real numbers, hence changing their magnitudes but leaving their phases intact. Here the twist is that we want simply to replace the magnitudes of the original, $\vert S[m, k]\vert$, with magnitudes obtained from the control input (call them $\vert T[m, k]\vert$, say). The necessary gain would thus be,

$$g[m, k] = {{\vert T[m, k]\vert}\over{\vert S[m, k]\vert}}$$

In practice it is best to limit the gain to some maximum value (which might depend on frequency) since otherwise channels containing nothing but noise, sidelobes, or even truncation error might be raised to audibility. So a suitable limiting function is applied to the gain before using it.