



Next: Real outputs from complex
Up: Elementary filters
Previous: Elementary recirculating filter
Contents
Index
We can use the recirculating and non-recirculating filters developed here to
create a
compound filter by putting several elementary ones in series. If the parameters
of the non-recirculating ones (of the first type) are
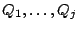 and those of the recirculating ones are
and those of the recirculating ones are
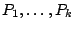 , then putting
them all in series, in any order, will give the transfer function:
, then putting
them all in series, in any order, will give the transfer function:
The frequency response of the resulting compound filter is the product of
those of
the elementary ones. (One could also combine elementary filters by adding
their outputs, or making more complicated networks of them; but for most
purposes the series configuration is the easiest one to work with.)
Miller Puckette
2006-12-30
![]() and those of the recirculating ones are
and those of the recirculating ones are
![]() , then putting
them all in series, in any order, will give the transfer function:
, then putting
them all in series, in any order, will give the transfer function: