Pitch shifting

A favorite use of variable delay lines is to alter the pitch of an incoming sound using the Doppler effect. It may be desirable to alter the pitch variably (randomly or periodically, for example), or else to maintain a fixed musical interval of transposition over a length of time.

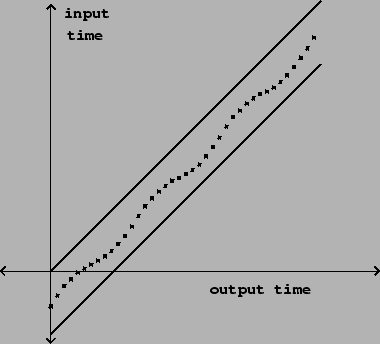
Returning to Figure 7.17, we see that with a single variable delay line we can maintain any desired pitch shift for a limited interval of time, but if we wish to sustain a fixed transposition we will always eventually land outside the diagonal strip of admissible delay times. In the simplest scenario, we simply vary the transposition up and down so as to remain in the strip.

Figure 7.19: Vibrato using a variable delay line. Since the pitch shift alternates between upward and downward, it is possible to maintain it without drifting outside the strip of admissible delay.

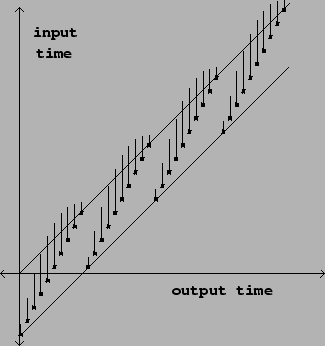
This works, for example, if we wish to apply vibrato to a sound as shown in Figure 7.19. Here the delay function is

$$d[n] = {d_0} + a \cos(\omega n)$$

where $d_0$ is the average delay, $a$ is the amplitude of variation about the average delay, and $\omega$ is an angular frequency. The Momentary Transposition (Page ), is approximately

$$t = 1 + a \omega \cos(\omega n - \pi/2)$$

This ranges in value between $1 - a \omega$ and $1 + a \omega$.

Figure 7.20: Piecewise linear delay functions to maintain a constant transposition (except at the points of discontinuity). The outputs are enveloped as suggested by the bars above each point, to smooth the output at the points of discontinuity in delay time.

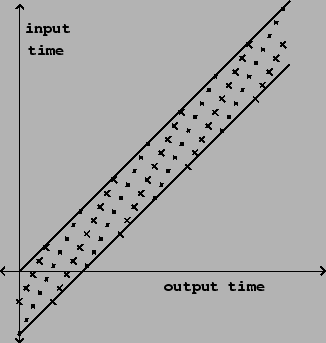
Suppose, on the other hand, that we wish to maintain a constant transposition over a longer interval of time. In this case we can't maintain the transposition forever, but it is still possible to maintain it over fixed intervals of time broken by discontinuous changes, as shown in Figure 7.20. The delay time is the output of a suitably normalized sawtooth function, and the output of the variable delay line is enveloped as shown in the figure to avoid discontinuities.

Figure 7.21: Using a variable delay line as a pitch shifter. The sawtooth wave creates a smoothly increasing or decreasing delay time. The output of the delay line is enveloped to avoid discontinuities. Another copy of the same diagram should run 180 degrees ($\pi$ radians) out of phase with this one.

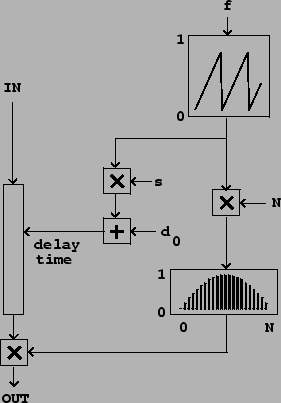This is accomplished as shown in Figure 7.21. The output of the sawtooth generator is used in two ways. First it is adjusted to run between the bounds ${d_0}$ and ${d_0}+s$, and this adjusted sawtooth controls the delay time, in samples. The initial delay $d_0$ should be at least enough to make the variable delay feasible; for four-point interpolation it must be at least one sample. Larger values of $d_0$ add a constant, additional delay to the output; this is usually offered as a control in a pitch shifter since it is essentially free. The quantity $s$ is sometimes called the window size. It corresponds roughly to the sample length in a looping sampler (Section 2.2).

The sawtooth output is also used to envelope the output in exactly the same way as in the enveloped wavetable sampler of Figure 2.7 (Page ). The envelope is zero at the points where the sawtooth wraps around, and in between, rises smoothly to a maximum value of 1 (for unit gain).

If the frequency of the sawtooth wave is $f$ (in cycles per second), then its value sweeps from 0 to 1 every $R/f$ samples (where $R$ is the sample rate). The difference between successive values is thus $f/R$. If we let $x[n]$ denote the output of the sawtooth oscillator, then

$$x[n+1] - x[n] = {f \over R}$$

(except at the wraparound points). If we adjust the output range of the wavetable oscillator to the value $s$ (as is done in the figure) we get a new slope:

$$s \cdot x[n+1] - s \cdot x[n] = {{sf} \over R}$$

Adding the constant $d_0$ has no effect on this slope. The Momentary Transposition (Page ) is then:

$$t = 1 - {{sf} \over R}$$

To complete the design of the pitch shifter we must add the other copy halfway out of phase. This gives rise to a delay reading pattern as shown in Figure 7.22.

Figure 7.22: The pitch shifter's delay reading pattern using two delay lines, so that one is at maximum amplitude exactly when the other is switching.

The pitch shifter can transpose either upward (using negative sawtooth frequencies, as in the figure) or downward, using positive ones. Pitch shift is usually controlled by changing $f$ with $s$ fixed. To get a desired transposition interval $t$, set

$$f = {{(t - 1) R} \over s}$$

The window size $s$ should be chosen small enough, if possible, so that the two delayed copies ($s/2$ samples apart) do not sound as distinct echoes. However, very small values of $s$ will force $f$ upward; values of $f$ greater than about 5 Hertz result in very audible modulation. So if very large transpositions are required, the value of $s$ may need to be increased. Typical values range from 30 to 100 milliseconds (about $R/30$ to $R/10$ samples).

Although the frequency may be changed at will, even discontinuously, $s$ must be changed more carefully. A possible solution is to mute the output while changing $s$ discontinuously; alternatively, $s$ may be ramped continuously but this causes hard-to-control Doppler shifts.

A good choice of envelope is one half cycle of a sinusoid. If we assume on average that the two delay outputs are uncorrelated (Page ), the signal power from the two delay lines, after enveloping, will add to a constant (since the sum of squares of the two envelopes is one).

Many variations exist on this pitch shifting algorithm. One classic variant uses a single delay line, with no enveloping at all. In this situation it is necessary to choose the point at which the delay time jumps, and the point it jumps to, so that the output stays continuous. For example, one could find a point where the output signal passes through zero (a "zero crossing") and jump discontinuously to another one. Using only one delay line has the advantage that the signal output sounds more "present". A disadvantage is that, since the delay time is a function of input signal value, the output is no longer a linear function of the input, so non-periodic inputs can give rise to artifacts such as difference tones.